Projects
Nono OSU! Keyboard

为音乐游戏OSU设计的机械键盘方案
Keyboard for OSU
LabelPlus - Easy comic translation tool
标号器+ 漫画翻译辅助工具. 减少翻译工作交接成本. 导出文本至ps.
A Easy tool for comic translation. Reduce communication costs of translator. Export text to Photoshop..
Blogs
将VPS作为家庭NAS的IPv4入口
目前家庭网络接入,常有IPv6公网但无IPv4公网地址,在家庭以外的网络环境可能仅有IPv4,但又需要访问家中的NAS;本文演示,如何用便宜的NAT-VPS作为家庭NAS的IPv4入口。
将Pro Micro 5v改为3v3版本
Pro Micro是一块Atmega32u4的Arduino开发板。
手上只有Pro Micro 5v,临时需要改成3.3v,本以为很简单,只是改个LDO就行了,没想到也折腾了一个晚上,所以简单记录一下。
WireGuard配置实例
因为家庭宽带没有IPv4,NAS在外无法方案,所以买了个VPS做流量转发,又因为VPS只有IPv4网络,所以先组VPN与NAS网络互通。
WireGuard和OpenVPN、Zerotier之类功能类似,就是虚拟局域网,相较竞品的特点就是极简,使用简单、功能简单。
不请装修公司的住宅装修日志
装修是大事,普通人一辈子也没几次装修的机会,不请装修公司,自己做工头难免踩坑,相信会是宝贵的实践经验,所以以日志的形式记录下来。 持续更新中…
在Photoshop的JS脚本中获取区域的颜色值
最近在完善 LabelPlus 的 Photoshop脚本 中的漫画对话框涂白功能,这功能需要获取文字附近位置的背景色,用背景色覆盖文字。
但PS中没有直接提供获取区域颜色的API,甚至没有获取像素颜色的API。经过摸索,找到了一种变通的方法——用R/G/B通道的直方图,获取区域大致的颜色值。
网易云音乐Linux版诸多问题解决办法
官方迟迟不修bug——无法播放无损音乐、无法用输入法、DPI问题。网上各种 workaround,用的人多就是好,这里简单汇总一下,目前2021-08-02的官方最新版本是1.2.1。
做了个包上传 AUR,修了无损音乐、输入法问题:netease-cloud-music-workarounds (更新:AUR中的netease-cloud-music已经修复了无法播放FLAC、输入法问题,这个包将被弃置、删除)
Linux下使用声笔系列码
声笔系列码是一系列顶功输入法,基于 RIME 输入法框架开发,为了实现顶功和aeiou键选重的特性,对 librime 进行了大量魔改,要想在 Linux 上用起,需要自己重新编译安装魔改后的 librime。
这篇文章会简单走一遍安装配置流程,如果你想在 Linux 下使用声笔系列码,应该会对你有帮助。

探索c-capnproto用于嵌入式工程的可行性
当前MCU上与外部交互的应用层协议,一般都是开发者手动编、解的简单二进制协议;用到序列化格式来做协议的需求,是IoT快速发展后才开始的,比如一些设备会用到JSON。
手头维护的硬件产品,应用协议已经很复杂了,一个二进制协议,实现、写文档都是麻烦事。所以我一直在探索一个快速、适合嵌入式应用的序列化格式方案,试图减轻开发负担。
Cap’n Proto是种快速数据交换格式,目标是数据快速交换、做RPC,由于它的格式在内存中能直接读、写,省略了编、解码的开销,所以相比google的protobuf快。c-capnproto是它在C中的实现。
这篇文章的目标是:研究c-capnproto的基本用法、评估将它用于嵌入式环境的可能性。
搭建树莓派持续集成环境
正在做的树莓派应用需要做持续集成,需要挂一台实机跑CI runner吗,不,官方提供了一个的docker镜象raspbian/stretch,利用QEMU执行ARM,可以让x86计算机能直接用上raspbian环境。
这篇文章记录了一次树莓派持续集成环境的搭建过程,用的CI是gitlab-ci。
MacOS-Vitrualbox虚拟机安装小记
工作需要为USB设备适配MacOS,手头没mac设备,总借同事的也不是个办法,于是打算自己装个。
上github搜了一下,果然有现成的脚本,用它成功安装了MacOS虚拟机,这里记录一下过程。
键鼠共享软件Barrier编译和使用小记
Barrier可以让多台桌面计算机,通过网络共享同一套鼠标键盘,从synergy-core项目fork而来,基于QT,支持主流桌面操作系统。
这篇文章记录Barrier的使用方法,包括编译、安装、配置。
用MkDocs搭建个人wiki
之前用了一段Hexo搭的个人Wiki,随着页数越来越多,Hexo生成页面就有点吃不消了,后来尝试了MkDocs感觉很适合这个场景,除了搜索功能对中文的支持比较弱以外,表现很棒,无论是易用度、生成速度。
我的常用软件_工作方式
摸鱼写一篇文 记录自己觉得用起来很方便的工具、工作方式。
2015-11-26 初版
2018-12-03 更新
2019-09-22 工作环境基本在Linux这边之后,做点补充
2020-04-19 补充数据同步、效率提升
用Hexo搭建个人Wiki
注意!!文章已过时,由于Hexo生成页面速度慢、页面多了还会爆内存,搭建方法也麻烦,已经不推荐用Hexo搭wiki,请参考另一篇使用MkDocs搭建的
为什么需要个人Wiki?整理知识,数字时代前人们做纸制笔记、做剪报;现在普遍用博客做笔记、everynote做文章收藏。
工作学习中产生的笔记总会是零碎的片段,尴尬的是——博客本应是展示水平的地方,不适合放零散的笔记;everynote、有道云笔记之类的产品虽然收藏功能强大,但配不上它们作为“笔记”的名头,知识难以归类、编辑体验一般。
细化一下我们的需求:
- 方便编辑,增加文章必须简单;
- 词条的分类必须灵活,因为知识体系随着时间推移会越来越完善,之前的分类在一段时间后就不适用了;
- 需要用笔记时能快速提取,最好支持多种客户端。
纠结了很长一段时间,总算是组了一套找到了贴合这些需求的方案:用Hexo+Wiki模板做渲染,用文件夹组织层次结构,用Typora做Markdown编辑器,Webhook+CI服务器做自动构建、部署。
快速搭建github的webhook服务器
Git的Hook功能可以让仓库在某些条件触发下执行特定脚本,而各托管平台都实现了自家的Webhook功能,将这些事件通过Web API的形式向外发送事件通知,我们常用Webhook在服务器上做自动部署、持续集成等。
这里用快速搭建一个最小功能的Github Webhook Server,当有人向仓库推送东西时,服务器会自动执行设定的脚本。
双拼加辅助码——低成本提升中文输入体验
好的输入体验应该是流畅、有节奏的,双拼+形码辅助是一种低成本提升中文输入体验的方法,适合人群:
- 已经比较熟悉键盘,但输入速度难进一步提升的人
- 厌烦了拼音输入法的重码,不想废眼睛废时间选字
- 痛恨某些输入法的广告,想转其他输入法但又不想降低输入体验的人

Newifi-d2路由器折腾笔记
朋友推荐了个适合当开发机的路由,某宝80多元的二手,MT7621AT@880MHz,512MB DDR3,32MB Flash,ROM和RAM都够大,那就开始折腾。
什么时候需要用RTOS?
想写篇关于小资源的嵌入式系统的编程架构搭建的文章,但一下子想不出从哪开始下笔。
毕竟技术是为了解决问题而存在的,要说清楚“怎么做”,得先知道“需要解决什么问题”。
这时候想起N年前看过个叫Mark3OS的RTOS的文档把“RTOS帮我们做了什么”这个问题给讲清楚了,于是直接翻译出来吧,下一篇会在此基础上扩展地讲。
P.S. 这个项目似乎已经停止维护了,网站也关了,毕竟没什么人用。。
windows上的包管理器chocolatey
win给人感觉,装什么都得下个安装程序一路next到底,有了choco这些工作就能自动完成了,舒爽:
1
2
3
4
5
6
7
8
C:\>choco install Python3
Chocolatey v0.10.11
Installing the following packages:
Python3
...
Installing 64-bit python3...
python3 has been installed.
...
GH60变身POKER3——仿poker3的TMK格式配列
笔者kbt race2入坑 主要看重便携
后来入了poker3 非常喜欢它的初始键位设计和alt+space将右下角的四个键变成方向键的功能
然而由于它的钢板和浇铸外壳 poker3虽小巧但重量感人
于是笔者下定决心入一块GH60再把配列改成类似poker3的方案
琢磨了一个晚上终于弄好了poker3配列 现在将他分享出来
2016-08-21 初版
2018-10-14 改进方案、增加小键盘布局,增加Github仓库链接
CPP深入学习笔记
大学期间听过CPP的课,之后就没怎么写过,顶多是有需要的时候看看别人的代码,这里简单做点记录。
计划系统性的补补:
- C++标准库、STL
- 设计模式
- Boost之类的常见库
(放弃了,CPP不是我现在该碰的东西)
小鹤音形二简词输入总结-以及RIME输入法用的二简词提示码表
二简词是小鹤双形码表的一个特色,比如aq=安全,能快速录入常见二字词。
但当以4字词组方式输入一个二简词时,输入法不会提示,所以就需要额外记忆了,所以这里使用正则表达式提取了小鹤双形的二级简码词 顺便总结了一下符号输入。
文末附上个RIME用的二简词提示码表。
制作一个能从各种ISO镜象启动的U盘
装机要用到各种工具u盘,手上只有一个u盘的时候总得费事格式化,如果直接把ISO镜象拖到U盘里按需选用就能方便很多。于是试着弄了个能灵活加载各种ISO镜象的U盘,这里记录一下过程。
windows下的Eclipse+JLink调试——ARM裸机开发环境搭建
在公司用着eclipse感觉挺不错
调试起来比emblock要舒服
用eclipse+arm-gcc+JLink的人越来越多了吧
仅记录一下配置方法
用git做web应用自动部署
准备要把shabao.io弄起来
用git往web server上push来迭代挺方便的
参考了网上的文章还是踩了些坑 这里简要记一下步骤(服务器用的ubuntu)
在eclipse中使用openOCD+CMSIS_DAP进行ARM在线调试
购入CMSIS-DAP仿真器 摸索摸索(抛弃盗版Jlink的日子要来了..
这里记录win下使用eclipse+openOCD+cmsis_dap调试arm程序的配置方法
嵌入式软件开发学习路线
在这个领域学习过程中碰了不少壁
大学里的三年里 笔者也只能算是刚入门
这篇文章会随着我自己的学习不断地更新
这是我觉得比较好的学习路线 希望初学者能少走弯路
如有说得不对的地方 还请帮忙指正,谢谢
Nono OSU! Keyboard

为音乐游戏OSU设计的机械键盘方案
Keyboard for OSU
LabelPlus - Easy comic translation tool
标号器+ 漫画翻译辅助工具. 减少翻译工作交接成本. 导出文本至ps.
A Easy tool for comic translation. Reduce communication costs of translator. Export text to Photoshop..
Blogs
将VPS作为家庭NAS的IPv4入口
目前家庭网络接入,常有IPv6公网但无IPv4公网地址,在家庭以外的网络环境可能仅有IPv4,但又需要访问家中的NAS;本文演示,如何用便宜的NAT-VPS作为家庭NAS的IPv4入口。
将Pro Micro 5v改为3v3版本
Pro Micro是一块Atmega32u4的Arduino开发板。
手上只有Pro Micro 5v,临时需要改成3.3v,本以为很简单,只是改个LDO就行了,没想到也折腾了一个晚上,所以简单记录一下。
WireGuard配置实例
因为家庭宽带没有IPv4,NAS在外无法方案,所以买了个VPS做流量转发,又因为VPS只有IPv4网络,所以先组VPN与NAS网络互通。
WireGuard和OpenVPN、Zerotier之类功能类似,就是虚拟局域网,相较竞品的特点就是极简,使用简单、功能简单。
不请装修公司的住宅装修日志
装修是大事,普通人一辈子也没几次装修的机会,不请装修公司,自己做工头难免踩坑,相信会是宝贵的实践经验,所以以日志的形式记录下来。 持续更新中…
在Photoshop的JS脚本中获取区域的颜色值
最近在完善 LabelPlus 的 Photoshop脚本 中的漫画对话框涂白功能,这功能需要获取文字附近位置的背景色,用背景色覆盖文字。
但PS中没有直接提供获取区域颜色的API,甚至没有获取像素颜色的API。经过摸索,找到了一种变通的方法——用R/G/B通道的直方图,获取区域大致的颜色值。
网易云音乐Linux版诸多问题解决办法
官方迟迟不修bug——无法播放无损音乐、无法用输入法、DPI问题。网上各种 workaround,用的人多就是好,这里简单汇总一下,目前2021-08-02的官方最新版本是1.2.1。
做了个包上传 AUR,修了无损音乐、输入法问题:netease-cloud-music-workarounds (更新:AUR中的netease-cloud-music已经修复了无法播放FLAC、输入法问题,这个包将被弃置、删除)
Linux下使用声笔系列码
声笔系列码是一系列顶功输入法,基于 RIME 输入法框架开发,为了实现顶功和aeiou键选重的特性,对 librime 进行了大量魔改,要想在 Linux 上用起,需要自己重新编译安装魔改后的 librime。
这篇文章会简单走一遍安装配置流程,如果你想在 Linux 下使用声笔系列码,应该会对你有帮助。

探索c-capnproto用于嵌入式工程的可行性
当前MCU上与外部交互的应用层协议,一般都是开发者手动编、解的简单二进制协议;用到序列化格式来做协议的需求,是IoT快速发展后才开始的,比如一些设备会用到JSON。
手头维护的硬件产品,应用协议已经很复杂了,一个二进制协议,实现、写文档都是麻烦事。所以我一直在探索一个快速、适合嵌入式应用的序列化格式方案,试图减轻开发负担。
Cap’n Proto是种快速数据交换格式,目标是数据快速交换、做RPC,由于它的格式在内存中能直接读、写,省略了编、解码的开销,所以相比google的protobuf快。c-capnproto是它在C中的实现。
这篇文章的目标是:研究c-capnproto的基本用法、评估将它用于嵌入式环境的可能性。
搭建树莓派持续集成环境
正在做的树莓派应用需要做持续集成,需要挂一台实机跑CI runner吗,不,官方提供了一个的docker镜象raspbian/stretch,利用QEMU执行ARM,可以让x86计算机能直接用上raspbian环境。
这篇文章记录了一次树莓派持续集成环境的搭建过程,用的CI是gitlab-ci。
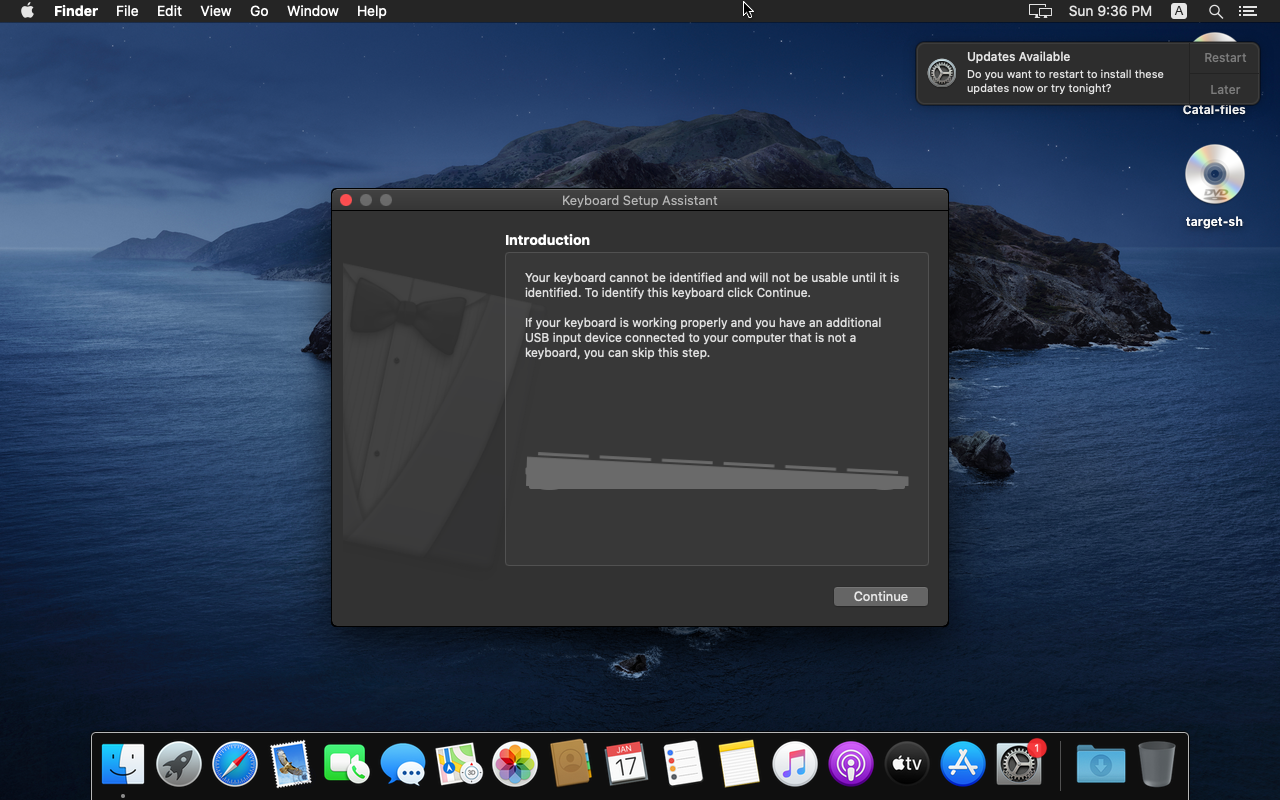
MacOS-Vitrualbox虚拟机安装小记
工作需要为USB设备适配MacOS,手头没mac设备,总借同事的也不是个办法,于是打算自己装个。
上github搜了一下,果然有现成的脚本,用它成功安装了MacOS虚拟机,这里记录一下过程。

键鼠共享软件Barrier编译和使用小记
Barrier可以让多台桌面计算机,通过网络共享同一套鼠标键盘,从synergy-core项目fork而来,基于QT,支持主流桌面操作系统。
这篇文章记录Barrier的使用方法,包括编译、安装、配置。
用MkDocs搭建个人wiki
之前用了一段Hexo搭的个人Wiki,随着页数越来越多,Hexo生成页面就有点吃不消了,后来尝试了MkDocs感觉很适合这个场景,除了搜索功能对中文的支持比较弱以外,表现很棒,无论是易用度、生成速度。
我的常用软件_工作方式
摸鱼写一篇文 记录自己觉得用起来很方便的工具、工作方式。
2015-11-26 初版
2018-12-03 更新
2019-09-22 工作环境基本在Linux这边之后,做点补充
2020-04-19 补充数据同步、效率提升
用Hexo搭建个人Wiki
注意!!文章已过时,由于Hexo生成页面速度慢、页面多了还会爆内存,搭建方法也麻烦,已经不推荐用Hexo搭wiki,请参考另一篇使用MkDocs搭建的
为什么需要个人Wiki?整理知识,数字时代前人们做纸制笔记、做剪报;现在普遍用博客做笔记、everynote做文章收藏。
工作学习中产生的笔记总会是零碎的片段,尴尬的是——博客本应是展示水平的地方,不适合放零散的笔记;everynote、有道云笔记之类的产品虽然收藏功能强大,但配不上它们作为“笔记”的名头,知识难以归类、编辑体验一般。
细化一下我们的需求:
- 方便编辑,增加文章必须简单;
- 词条的分类必须灵活,因为知识体系随着时间推移会越来越完善,之前的分类在一段时间后就不适用了;
- 需要用笔记时能快速提取,最好支持多种客户端。
纠结了很长一段时间,总算是组了一套找到了贴合这些需求的方案:用Hexo+Wiki模板做渲染,用文件夹组织层次结构,用Typora做Markdown编辑器,Webhook+CI服务器做自动构建、部署。
快速搭建github的webhook服务器
Git的Hook功能可以让仓库在某些条件触发下执行特定脚本,而各托管平台都实现了自家的Webhook功能,将这些事件通过Web API的形式向外发送事件通知,我们常用Webhook在服务器上做自动部署、持续集成等。
这里用快速搭建一个最小功能的Github Webhook Server,当有人向仓库推送东西时,服务器会自动执行设定的脚本。
双拼加辅助码——低成本提升中文输入体验
好的输入体验应该是流畅、有节奏的,双拼+形码辅助是一种低成本提升中文输入体验的方法,适合人群:
- 已经比较熟悉键盘,但输入速度难进一步提升的人
- 厌烦了拼音输入法的重码,不想废眼睛废时间选字
- 痛恨某些输入法的广告,想转其他输入法但又不想降低输入体验的人

Newifi-d2路由器折腾笔记
朋友推荐了个适合当开发机的路由,某宝80多元的二手,MT7621AT@880MHz,512MB DDR3,32MB Flash,ROM和RAM都够大,那就开始折腾。
什么时候需要用RTOS?
想写篇关于小资源的嵌入式系统的编程架构搭建的文章,但一下子想不出从哪开始下笔。
毕竟技术是为了解决问题而存在的,要说清楚“怎么做”,得先知道“需要解决什么问题”。
这时候想起N年前看过个叫Mark3OS的RTOS的文档把“RTOS帮我们做了什么”这个问题给讲清楚了,于是直接翻译出来吧,下一篇会在此基础上扩展地讲。
P.S. 这个项目似乎已经停止维护了,网站也关了,毕竟没什么人用。。
windows上的包管理器chocolatey
win给人感觉,装什么都得下个安装程序一路next到底,有了choco这些工作就能自动完成了,舒爽:
1
2
3
4
5
6
7
8
C:\>choco install Python3
Chocolatey v0.10.11
Installing the following packages:
Python3
...
Installing 64-bit python3...
python3 has been installed.
...
GH60变身POKER3——仿poker3的TMK格式配列
笔者kbt race2入坑 主要看重便携
后来入了poker3 非常喜欢它的初始键位设计和alt+space将右下角的四个键变成方向键的功能
然而由于它的钢板和浇铸外壳 poker3虽小巧但重量感人
于是笔者下定决心入一块GH60再把配列改成类似poker3的方案
琢磨了一个晚上终于弄好了poker3配列 现在将他分享出来
2016-08-21 初版
2018-10-14 改进方案、增加小键盘布局,增加Github仓库链接
CPP深入学习笔记
大学期间听过CPP的课,之后就没怎么写过,顶多是有需要的时候看看别人的代码,这里简单做点记录。
计划系统性的补补:
- C++标准库、STL
- 设计模式
- Boost之类的常见库
(放弃了,CPP不是我现在该碰的东西)
小鹤音形二简词输入总结-以及RIME输入法用的二简词提示码表
二简词是小鹤双形码表的一个特色,比如aq=安全,能快速录入常见二字词。
但当以4字词组方式输入一个二简词时,输入法不会提示,所以就需要额外记忆了,所以这里使用正则表达式提取了小鹤双形的二级简码词 顺便总结了一下符号输入。
文末附上个RIME用的二简词提示码表。
制作一个能从各种ISO镜象启动的U盘
装机要用到各种工具u盘,手上只有一个u盘的时候总得费事格式化,如果直接把ISO镜象拖到U盘里按需选用就能方便很多。于是试着弄了个能灵活加载各种ISO镜象的U盘,这里记录一下过程。
windows下的Eclipse+JLink调试——ARM裸机开发环境搭建
在公司用着eclipse感觉挺不错
调试起来比emblock要舒服
用eclipse+arm-gcc+JLink的人越来越多了吧
仅记录一下配置方法
用git做web应用自动部署
准备要把shabao.io弄起来
用git往web server上push来迭代挺方便的
参考了网上的文章还是踩了些坑 这里简要记一下步骤(服务器用的ubuntu)
在eclipse中使用openOCD+CMSIS_DAP进行ARM在线调试
购入CMSIS-DAP仿真器 摸索摸索(抛弃盗版Jlink的日子要来了..
这里记录win下使用eclipse+openOCD+cmsis_dap调试arm程序的配置方法
嵌入式软件开发学习路线
在这个领域学习过程中碰了不少壁
大学里的三年里 笔者也只能算是刚入门
这篇文章会随着我自己的学习不断地更新
这是我觉得比较好的学习路线 希望初学者能少走弯路
如有说得不对的地方 还请帮忙指正,谢谢
将VPS作为家庭NAS的IPv4入口
目前家庭网络接入,常有IPv6公网但无IPv4公网地址,在家庭以外的网络环境可能仅有IPv4,但又需要访问家中的NAS;本文演示,如何用便宜的NAT-VPS作为家庭NAS的IPv4入口。
将Pro Micro 5v改为3v3版本
Pro Micro是一块Atmega32u4的Arduino开发板。
手上只有Pro Micro 5v,临时需要改成3.3v,本以为很简单,只是改个LDO就行了,没想到也折腾了一个晚上,所以简单记录一下。
WireGuard配置实例
因为家庭宽带没有IPv4,NAS在外无法方案,所以买了个VPS做流量转发,又因为VPS只有IPv4网络,所以先组VPN与NAS网络互通。
WireGuard和OpenVPN、Zerotier之类功能类似,就是虚拟局域网,相较竞品的特点就是极简,使用简单、功能简单。
不请装修公司的住宅装修日志
装修是大事,普通人一辈子也没几次装修的机会,不请装修公司,自己做工头难免踩坑,相信会是宝贵的实践经验,所以以日志的形式记录下来。 持续更新中…
在Photoshop的JS脚本中获取区域的颜色值
最近在完善 LabelPlus 的 Photoshop脚本 中的漫画对话框涂白功能,这功能需要获取文字附近位置的背景色,用背景色覆盖文字。
但PS中没有直接提供获取区域颜色的API,甚至没有获取像素颜色的API。经过摸索,找到了一种变通的方法——用R/G/B通道的直方图,获取区域大致的颜色值。
网易云音乐Linux版诸多问题解决办法
官方迟迟不修bug——无法播放无损音乐、无法用输入法、DPI问题。网上各种 workaround,用的人多就是好,这里简单汇总一下,目前2021-08-02的官方最新版本是1.2.1。
做了个包上传 AUR,修了无损音乐、输入法问题:netease-cloud-music-workarounds (更新:AUR中的netease-cloud-music已经修复了无法播放FLAC、输入法问题,这个包将被弃置、删除)
Linux下使用声笔系列码
声笔系列码是一系列顶功输入法,基于 RIME 输入法框架开发,为了实现顶功和aeiou键选重的特性,对 librime 进行了大量魔改,要想在 Linux 上用起,需要自己重新编译安装魔改后的 librime。
这篇文章会简单走一遍安装配置流程,如果你想在 Linux 下使用声笔系列码,应该会对你有帮助。

探索c-capnproto用于嵌入式工程的可行性
当前MCU上与外部交互的应用层协议,一般都是开发者手动编、解的简单二进制协议;用到序列化格式来做协议的需求,是IoT快速发展后才开始的,比如一些设备会用到JSON。
手头维护的硬件产品,应用协议已经很复杂了,一个二进制协议,实现、写文档都是麻烦事。所以我一直在探索一个快速、适合嵌入式应用的序列化格式方案,试图减轻开发负担。
Cap’n Proto是种快速数据交换格式,目标是数据快速交换、做RPC,由于它的格式在内存中能直接读、写,省略了编、解码的开销,所以相比google的protobuf快。c-capnproto是它在C中的实现。
这篇文章的目标是:研究c-capnproto的基本用法、评估将它用于嵌入式环境的可能性。
搭建树莓派持续集成环境
正在做的树莓派应用需要做持续集成,需要挂一台实机跑CI runner吗,不,官方提供了一个的docker镜象raspbian/stretch,利用QEMU执行ARM,可以让x86计算机能直接用上raspbian环境。
这篇文章记录了一次树莓派持续集成环境的搭建过程,用的CI是gitlab-ci。
MacOS-Vitrualbox虚拟机安装小记
工作需要为USB设备适配MacOS,手头没mac设备,总借同事的也不是个办法,于是打算自己装个。
上github搜了一下,果然有现成的脚本,用它成功安装了MacOS虚拟机,这里记录一下过程。

键鼠共享软件Barrier编译和使用小记
Barrier可以让多台桌面计算机,通过网络共享同一套鼠标键盘,从synergy-core项目fork而来,基于QT,支持主流桌面操作系统。
这篇文章记录Barrier的使用方法,包括编译、安装、配置。
用MkDocs搭建个人wiki
之前用了一段Hexo搭的个人Wiki,随着页数越来越多,Hexo生成页面就有点吃不消了,后来尝试了MkDocs感觉很适合这个场景,除了搜索功能对中文的支持比较弱以外,表现很棒,无论是易用度、生成速度。
我的常用软件_工作方式
摸鱼写一篇文 记录自己觉得用起来很方便的工具、工作方式。
2015-11-26 初版
2018-12-03 更新
2019-09-22 工作环境基本在Linux这边之后,做点补充
2020-04-19 补充数据同步、效率提升
用Hexo搭建个人Wiki
注意!!文章已过时,由于Hexo生成页面速度慢、页面多了还会爆内存,搭建方法也麻烦,已经不推荐用Hexo搭wiki,请参考另一篇使用MkDocs搭建的
为什么需要个人Wiki?整理知识,数字时代前人们做纸制笔记、做剪报;现在普遍用博客做笔记、everynote做文章收藏。
工作学习中产生的笔记总会是零碎的片段,尴尬的是——博客本应是展示水平的地方,不适合放零散的笔记;everynote、有道云笔记之类的产品虽然收藏功能强大,但配不上它们作为“笔记”的名头,知识难以归类、编辑体验一般。
细化一下我们的需求:
- 方便编辑,增加文章必须简单;
- 词条的分类必须灵活,因为知识体系随着时间推移会越来越完善,之前的分类在一段时间后就不适用了;
- 需要用笔记时能快速提取,最好支持多种客户端。
纠结了很长一段时间,总算是组了一套找到了贴合这些需求的方案:用Hexo+Wiki模板做渲染,用文件夹组织层次结构,用Typora做Markdown编辑器,Webhook+CI服务器做自动构建、部署。
快速搭建github的webhook服务器
Git的Hook功能可以让仓库在某些条件触发下执行特定脚本,而各托管平台都实现了自家的Webhook功能,将这些事件通过Web API的形式向外发送事件通知,我们常用Webhook在服务器上做自动部署、持续集成等。
这里用快速搭建一个最小功能的Github Webhook Server,当有人向仓库推送东西时,服务器会自动执行设定的脚本。
双拼加辅助码——低成本提升中文输入体验
好的输入体验应该是流畅、有节奏的,双拼+形码辅助是一种低成本提升中文输入体验的方法,适合人群:
- 已经比较熟悉键盘,但输入速度难进一步提升的人
- 厌烦了拼音输入法的重码,不想废眼睛废时间选字
- 痛恨某些输入法的广告,想转其他输入法但又不想降低输入体验的人

Newifi-d2路由器折腾笔记
朋友推荐了个适合当开发机的路由,某宝80多元的二手,MT7621AT@880MHz,512MB DDR3,32MB Flash,ROM和RAM都够大,那就开始折腾。
什么时候需要用RTOS?
想写篇关于小资源的嵌入式系统的编程架构搭建的文章,但一下子想不出从哪开始下笔。
毕竟技术是为了解决问题而存在的,要说清楚“怎么做”,得先知道“需要解决什么问题”。
这时候想起N年前看过个叫Mark3OS的RTOS的文档把“RTOS帮我们做了什么”这个问题给讲清楚了,于是直接翻译出来吧,下一篇会在此基础上扩展地讲。
P.S. 这个项目似乎已经停止维护了,网站也关了,毕竟没什么人用。。
windows上的包管理器chocolatey
win给人感觉,装什么都得下个安装程序一路next到底,有了choco这些工作就能自动完成了,舒爽:
1 | C:\>choco install Python3 |
GH60变身POKER3——仿poker3的TMK格式配列
笔者kbt race2入坑 主要看重便携
后来入了poker3 非常喜欢它的初始键位设计和alt+space将右下角的四个键变成方向键的功能
然而由于它的钢板和浇铸外壳 poker3虽小巧但重量感人
于是笔者下定决心入一块GH60再把配列改成类似poker3的方案
琢磨了一个晚上终于弄好了poker3配列 现在将他分享出来
2016-08-21 初版
2018-10-14 改进方案、增加小键盘布局,增加Github仓库链接
CPP深入学习笔记
大学期间听过CPP的课,之后就没怎么写过,顶多是有需要的时候看看别人的代码,这里简单做点记录。
计划系统性的补补:
- C++标准库、STL
- 设计模式
- Boost之类的常见库
(放弃了,CPP不是我现在该碰的东西)
小鹤音形二简词输入总结-以及RIME输入法用的二简词提示码表
二简词是小鹤双形码表的一个特色,比如aq=安全,能快速录入常见二字词。
但当以4字词组方式输入一个二简词时,输入法不会提示,所以就需要额外记忆了,所以这里使用正则表达式提取了小鹤双形的二级简码词 顺便总结了一下符号输入。
文末附上个RIME用的二简词提示码表。
制作一个能从各种ISO镜象启动的U盘
装机要用到各种工具u盘,手上只有一个u盘的时候总得费事格式化,如果直接把ISO镜象拖到U盘里按需选用就能方便很多。于是试着弄了个能灵活加载各种ISO镜象的U盘,这里记录一下过程。
windows下的Eclipse+JLink调试——ARM裸机开发环境搭建
在公司用着eclipse感觉挺不错
调试起来比emblock要舒服
用eclipse+arm-gcc+JLink的人越来越多了吧
仅记录一下配置方法
用git做web应用自动部署
准备要把shabao.io弄起来
用git往web server上push来迭代挺方便的
参考了网上的文章还是踩了些坑 这里简要记一下步骤(服务器用的ubuntu)
在eclipse中使用openOCD+CMSIS_DAP进行ARM在线调试
购入CMSIS-DAP仿真器 摸索摸索(抛弃盗版Jlink的日子要来了..
这里记录win下使用eclipse+openOCD+cmsis_dap调试arm程序的配置方法
嵌入式软件开发学习路线
在这个领域学习过程中碰了不少壁
大学里的三年里 笔者也只能算是刚入门
这篇文章会随着我自己的学习不断地更新
这是我觉得比较好的学习路线 希望初学者能少走弯路
如有说得不对的地方 还请帮忙指正,谢谢